Microsoft Excel 엑셀 복리 계산 방법 알아보기 일, 월, 연 복리

복합 이자는 은행의 기본 구성 요소 중 하나이며
투자 결과를 결정하는 가장 강력한 금융력 중 하나입니다.
회계학과 졸업생, 재무 분석가 또는 경험 많은 투자자가 아닌 이상
전문 재무 장부와 매뉴얼에서 개념을 파악하는 것이 다소 어려울 수 있습니다.
이 글의 목적은 쉽게 만드는 것입니다 :) 엑셀에서 복합 이자 공식을 사용하는 방법과
자신의 워크시트에 대한 범용 복합 이자 계산기를 만드는 방법도 배울 것입니다.

복리란 무엇입니까?
아주 간단한 용어로 이자에 대해 얻는 이자입니다.
더 정확하게 말하면, 최초 예금(원금)과 이전 기간에서 누적된 이자 모두에 대해 복리 이자가 발생합니다.
아마도 원금에만 계산되는 것으로 시작하는 것이 더 쉬울 수 있습니다.
예를 들어, 10달러를 은행 계좌에 넣었습니다.
연 7%의 금리로 1년 후 예금 가치는 얼마입니까?
정답은 $10.70(10 + 10*0.07 = 10.70)이며,
적립 이자는 $0.70입니다.
복리의 경우 각 기간마다 원금이 다릅니다.
은행은 벌어들인 이자를 돌려주지 않고 대신 원금 투자에 추가합니다.
이렇게 늘어난 금액은 다음 기간(계산기간)의 원금이 되고 이자도 얻게 됩니다.
즉 원금뿐만 아니라 매 복리후생 기간마다 벌어들인 이자에 대한 이자도 얻게 됩니다.
저희의 예에서는 원금 10달러 외에 근로이자 0.70달러도 내년에 이자를 얻게 됩니다.
그렇다면 연간 7%의 복리 이자율로 2년 후 10달러의 예금 가치는 얼마입니까?
정답은 $11.45(10.7 + 10.7*0.07 = 11.45)이며,
근로 이자는 $1.45입니다.
보시다시피, 2년차 말에는 최초 10달러 보증금으로 0.70달러를 받았을 뿐만 아니라
1년차에 누적된 0.70달러 이자로 0.05달러를 벌었습니다.
엑셀에 대한 복합 이자를 계산하는 방법은 여러 가지가 있는데,
각각에 대해 자세히 논의하려고 합니다.
엑셀 복리 계산 방법
장기 투자는 부를 증가시키는 효과적인 전략이 될 수 있으며,
작은 예금이라도 시간이 지남에 따라 큰 차이를 만들 수 있습니다.
추가로 설명하는 엑셀 복합 이자 공식은 저축 전략을 효과적으로 작동시키는 데 도움이 될 것입니다.
최종적으로, 우리는 매일, 매주, 매월, 분기별 또는 연간으로 다양한 복합 기간을 가진
미래 가치를 계산하는 보편적인 공식을 만들 것입니다.
엑셀에 대한 연간 복리후생비 산정
복리후생 개념을 더 잘 이해하기 위해 이 튜토리얼의 시작 부분에서 논의한
매우 간단한 예부터 시작하여 엑셀에서 연간 복리후생을 계산하는 공식을 작성해 보겠습니다.
기억하시겠지만, 연 7%의 이자율로 $10를 투자하고 있으며,
연간 복리 후생이 어떻게 절감을 증가시키는지 알고 싶습니다.
연간 복리 이자 - 식 1
연간 복리 이자로 벌어들이는 금액을 계산하는 쉽고 간단한 방법은
공식을 사용하여 숫자를 백분율로 증가시키는 것입니다.
=Amount * (1 + %).
이 예제에서 공식은 다음과 같습니다.
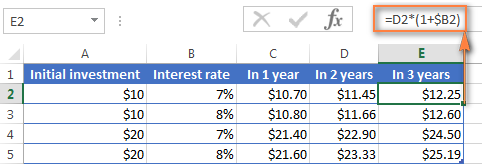
=A2*(1+$B2)
여기서 A2는 초기 보증금이고 B2는 연간 이자율입니다.
$ 기호를 사용하여 B열에 대한 참조를 수정하므로 주의하시기 바랍니다.
기억하시겠지만 1%는 백의 한 부분, 즉 0.01이므로 7%는 0.07이고
이것이 실제로 백분율이 엑셀에 저장되는 방식입니다.
이를 염두에 두고 10*(1+0.07) 또는 10*1.07의 간단한 계산을 수행하여
공식에 의해 반환되는 결과를 확인하고 1년 후 잔액이 실제로 10.70달러가 되는지 확인할 수 있습니다.
그리고 이제 2년 후 잔액을 계산해 보겠습니다.
그렇다면 연 7%의 이자율로 2년 동안 $10의 예금 가치는 얼마입니까?
정답은 11.45달러이며 같은 공식을 D열에 복사하면 구할 수 있습니다.

3년 후 은행 계좌에서 얼마의 돈을 찾을 수 있는지 계산하려면,
같은 공식을 E 열에 복사하기만 하면 12.25달러를 받을 수 있습니다.
엑셀 공식에 대해 어느 정도 경험이 있는 분들은 아마도
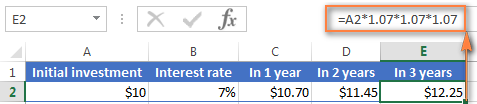
위 공식이 실제로 하는 일은 초기 보증금 10달러에 1.07을 세 번 곱하는 것이라는 것을 알아봤을 것입니다.
=10*1.07*1.07*1.07=12.25043
소수점 두 자리로 반올림하면 위 스크린샷의 셀 E2에서 보는 것과 같은 숫자 - $12.25입니다.
당연히 다음 공식을 사용하여 3년 후 잔액을 직접 계산할 수 있습니다.
=A2*1.07*1.07*1.07
연간 복리 이자 - 식 2
연간 복리식을 만드는 또 다른 방법은 각 연도의 근로 이자를 계산한 다음 초기 보증금에 추가하는 것입니다.
초기 예금이 셀 B1에 있고 셀 B2에 있는 연간 이자율이라고 가정하면 다음 공식이 효과가 있습니다.
=B1 + B1 * $B$2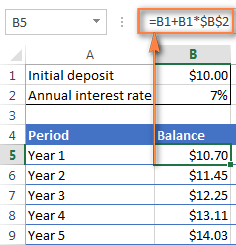
공식이 올바르게 작동하려면 다음 세부 정보를 참조하십시오.
$ 기호를 추가하여 연간 이자율 셀(B2의 경우)에 대한 참조를 수정합니다.
$B$2와 같이 절대 열과 절대 행이어야 합니다.
2차 연도(B6) 및 그 이후의 모든 연도에 대해 공식을 다음으로 변경합니다.
1차년도 잔액 + 1차년도 잔액 * 금리
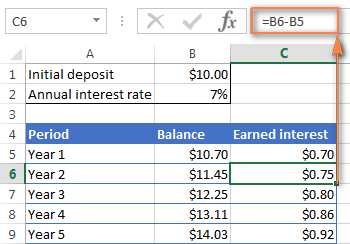
이 예에서는 셀 B6에 다음 공식을 입력한 다음 아래 스크린샷에 표시된 것처럼 다른 행으로 복사합니다.
=B5 + B5 * $B$2
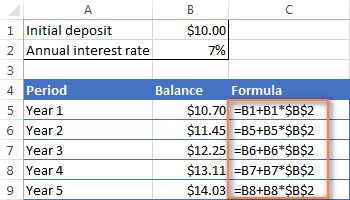
연간 복리로 실제로 얼마나 많은 이자를 얻었는지 알아보려면
1년 후 잔액(B5)에서 최초 예치금(B1)을 빼십시오.
이 공식은 C5로 넘어갑니다.
=B5-B1C6에서 2년 후 Balance에서 1년 후 Balance를 뺀 다음 공식을 다른 셀로 끕니다.
=B6-B5아래 스크린샷과 같이 수익 이자 증가를 확인해야 합니다.
위의 예들은 복합적인 관심사에 대한 아이디어를 잘 보여줍니다.
그렇지 않습니까? 그러나 어느 공식도 엑셀의 보편적인 복리 공식이라고 할 만큼 좋은 것은 없습니다.
첫째, 복리후생 빈도를 지정할 수 없기 때문이고,
둘째, 단순히 일정 기간과 이자율을 입력하는 것이 아니라
전체 표를 구축해야 하기 때문입니다.
자, 한 걸음 더 나아가 연간, 분기별, 월간, 주간 또는 일일 복리로
얼마의 돈을 벌 것인지 계산할 수 있는 보편적 복리식을 엑셀에 만들어 보겠습니다.
일반 복리식
재무자문사는 복합이자가 투자에 미치는 영향을 분석할 때 일반적으로
투자의 미래가치(FV)를 결정하는 세 가지 요소를 고려합니다.
PV - 투자의 현재가치
i - 각 기별 이자율
n - 기간수
이러한 구성 요소를 알면 다음 공식을 사용하여 특정 복리 이자율로 투자의 미래 가치를 얻을 수 있습니다.
FV = PV * (1 + i)n
요점을 더 잘 설명하기 위해 몇 가지 간단한 예를 소개합니다.
예 1: 월 복리식
매월 복리 8% 이자율로 2,000달러를 투자하고 5년 후 투자 가치를 알고 싶다고 가정해 보겠습니다.
먼저 복합 이자 공식에 대한 구성 요소 목록을 작성합니다.
PV = $2,000
i = 연 8%, 매월 복리후생(0.08/12=00666667)
n = 5년 x 12개월 (5*12=60)
위의 숫자를 공식에 입력하면 다음과 같은 결과가 나옵니다.
= $2,000 * (1 + 0.8/12)5x12
또는
= $2,000 * 1.00666666760
또는
= $2,000 * 1.489845708 = $2,979.69
예 2: 일별 복리식
월별 복리 이자 사례가 잘 이해되어 이제 일상 복리에도 동일한 접근 방식을 사용할 수 있기를 바랍니다. 최초 투자액, 이자율, 기간 및 공식은 위의 예와 정확히 동일하며, 복리후생 기간만 다릅니다.
PV = $2,000
i = 연 8%, 매일 복리 (0.08/365 = 0.000219178)
n = 5년 x 365일 (5*365 = 1825)
위의 숫자를 복리 공식에 입력하면 다음과 같은 결과가 나옵니다.
=$2,000 * (1 + 0.000219178)1825 = $2,983.52
보시다시피, 일일 복리 이자의 경우 동일한 투자의 미래 가치가
월간 복리 이자의 미래 가치보다 약간 높습니다.
8% 금리는 매월이 아닌 매일 원금에 이자를 더해주기 때문입니다.
짐작하실 수 있듯이 월별 복리 결과는 연간 복리보다 높을 것입니다.
2024.06.03-Microsoft Excel이 새 셀을 삽입할 수 없음 오류를 수정하는 방법
2024.06.13-마이크로 소프트 깨진 워드 문서를 복구하는 방법을 알아보자
2024.06.03-손상된 Excel 파일을 쉽게 복구할 수 있는 방법을 알아보자
2024.06.18-Microsoft Excel 이자율을 알아보는 RATE 함수 사용해 보기
-
'IT 이것저것 > 엑셀 활용' 카테고리의 다른 글
| 엑셀 팁, 마소 엑셀로 차트를 형식화하는 방법을 알아보자 (1) | 2024.12.25 |
|---|---|
| 엑셀 팁, 엑셀의 IF 및 XLOOKUP 함수 대신에 사용 가능한 SWITCH 기능 (0) | 2024.11.06 |
| Microsoft Excel 이자율을 알아보는 RATE 함수 사용해 보기 (1) | 2024.08.27 |
| Microsoft Excel 오류를 잡아내는 ISERROR 함수 사용해 보기 (0) | 2024.08.26 |
| 엑셀을 이용해서 년월일 날짜로 요일을 구하여 보자 (1) | 2024.08.25 |




댓글
KaNonx카논님의
글이 좋았다면 응원을 보내주세요!
이 글이 도움이 됐다면, 응원 댓글을 써보세요. 블로거에게 지급되는 응원금은 새로운 창작의 큰 힘이 됩니다.
응원 댓글은 만 14세 이상 카카오계정 이용자라면 누구나 편하게 작성, 결제할 수 있습니다.
글 본문, 댓글 목록 등을 통해 응원한 팬과 응원 댓글, 응원금을 강조해 보여줍니다.
응원금은 앱에서는 인앱결제, 웹에서는 카카오페이 및 신용카드로 결제할 수 있습니다.